Efficient withdrawal strategies in retirement investing

The investment problem for individuals and households in the decumulation phase can be broadly defined as a combination of consumption and bequest goals, subject to a dollar budget defined in terms of initial wealth. One of the key challenges for financial advisers is to provide personalised advice to individuals as far as their retirement investment decisions are concerned.

The original Merton problem (Merton [1969, 1971]) does address the joint optimisation of investment and consumption decisions, but the analysis is cast in an extremely simplified setting and cannot be directly used to develop an actionable decisionmaking process for individuals in decumulation. On the other hand, many heuristic withdrawal rules exist such as the 3% (or 4%) rule, including more sophisticated rules (see Suri et al [2020]). Relatively little, however, is known about the interaction between withdrawal and investment strategies. Our specific goal is to identify whether some withdrawal strategies are more suitable than others as a function of the level of risk taking in the investment portfolio.

Maeso et al (2021) propose a formal analysis of efficient investment strategies for individuals and households in the decumulation phase of their life cycle. They create for that purpose a comprehensive and flexible framework that can be used to derive optimal investment decisions taking as given a stream of fixed income withdrawal cash flows in the presence of long-term care risk, with a relatively rich menu of investment opportunities that includes balanced funds, target date funds, equity indices but also annuity products, for which they use realistic market quotes. In what follows, we study the introduction of additional, more flexible, withdrawal strategies as an extension of the Maeso et al (2021) initial framework and focus on the joint optimisation of investment and withdrawal decisions.

To study this joint optimisation, we apply the framework to a 65-year-old woman who is already retired (and assumed to have just retired). We assume that if and when she experiences longterm care needs, she will need additional retirement income to secure a semiprivate room at a cost of $90,155 × (1 + 3.10%)t per year at date t, and an annual cost increase of 3.10%.[1] We invite the reader to refer to section 4 of Maeso et al (2021) for more details on how market and longevity risks are modelled.

Exhibit 1 illustrates the rationale of the framework as our 65-year-old starts her retirement with an initial wealth of $500,000 and a 4% initial target withdrawal rate. The target withdrawal rate increases by 2% year on year to adjust for cost of living, and we assume for simplicity that no life event occurs. The individual’s target withdrawal TW(t) at date t is equal to the initial target withdrawal rate times initial wealth in real terms. For illustrative purposes, we assume that she invests all her initial wealth in a balanced fund. At each date t, if the value of the balanced fund account at date t is sufficient, she withdraws her replacement income needs from this account. Otherwise, she withdraws the balance (possibly nothing) of the account.

Exhibit 1 – Illustration of the Framework Rationale

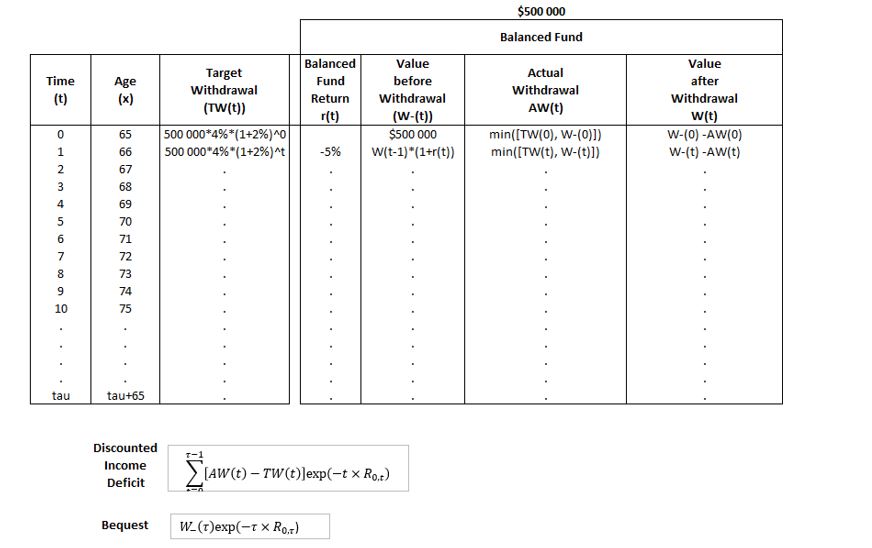
This exhibit displays how the main quantities of the framework are computed when the investment universe is made up of a balanced fund and life events are not taken into account.

The welfare function we use to determine the optimal investment strategy is based on two quantities, namely the discounted income deficit (ID in short, always negative), which is defined as actual withdrawals minus target withdrawals (given as 4% of initial wealth in the base case) and the discounted bequest (BS in short, always positive).

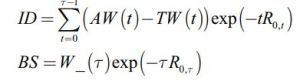
Here, TW(t) is the target withdrawal level at time t (given by 4% of the initial wealth in the base case, plus a possible cost-of-living adjustment), AW(t) is the actual withdrawal level at time t (which is equal to TW(t) where possible given the available wealth, and less than TW(t) otherwise), 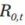is the annualised continuously compounded discount rate at time 0 for maturity t, W_(t) is the wealth available at time t before withdrawal, W(t) is the wealth available at time t after withdrawal, and is the uncertain date of death. Exhibit 1 shows how to calculate these quantities for a given Monte Carlo scenario. We define a welfare function that separates the contribution of the discounted bequest, which corresponds to the term Median (BS), and the contribution of the discounted income deficit, which is the term λVaR5% (ID) (strong risk-aversion with respect to income deficits). It is given by:

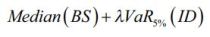
Where λ is a parameter that corresponds to the individual’s risk aversion.[2]

Description of the withdrawal strategies

We start by introducing notations that will be useful to define the different withdrawal strategies in what follows:

Date 0 – start of decumulation;

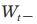– investor liquid wealth at time t before withdrawal;

ct – withdrawal amount in $ at time t; COLAt – percentage cost-of-living adjustment at time t;

WR – withdrawal rate as a percentage of the investor’s initial wealth;

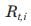– zero-coupon rate of maturity i years at time t;

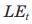– cost of the life event at time t;

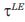: date of occurrence of the life event (equal to +∞ if no life event occurs).

We consider a 65-year-old female individual with initial wealth of $500,000. The investment universe is only made up of balanced funds with a X%/(1–X%) equity/bond allocation and annual rebalancing.3 We account for the presence of life event risk, which means that long-term care needs can occur with unresolved uncertainty with respect to the timing and severity of the event in terms of additional replacement income needs.

In the original version of the framework and in the presence of life events, the withdrawal strategy involves, where possible, withdrawing each year the same fixed withdrawal rate WR (say 3%, 4% or 5%) of the initial wealth 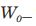with a 2% COLA component adjustment, which corresponds to the individual’s target level of replacement income to meet her expenses between dates t and t+1:

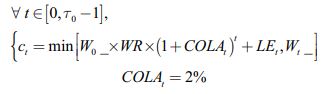
An attractive characteristic of this withdrawal strategy is that the individual has good visibility of the level of future withdrawals: if her current wealth at time t is sufficient, then she will withdraw the same amount of money in real or nominal terms until she dies. On the other hand, a drawback of this strategy is that she could be ruined before her death and consequently no longer able to meet her replacement income needs. This will happen in those scenarios of the Monte Carlo simulations where the portfolio wealth at time t is such that: 

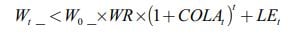
We will call this withdrawal strategy WS1.

Some authors, such as Bengen (1994), have focused on the maximum withdrawal rate with respect to the initial wealth for which the withdrawal strategy is sustainable for a 30-year time horizon, consistent with the intuition that a meaningful withdrawal strategy should lead to a low probability of the individual outliving her assets.

In addition to withdrawal strategy WS1, we also test two flexible withdrawal strategies, WS2 and WS3, where the individual cannot withdraw more than 4% of her initial wealth 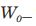with a 2% COLA component adjustment but will withdraw less than this amount if her current wealth 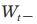minus the cost of life events 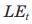is lower than a certain threshold. The main objective of these other withdrawal strategies is to minimise the probability of the individual outliving her assets by withdrawing less money in ‘bad states of the world’. The three withdrawal strategies WS1, WS2 and WS3 can be summarised as follows:

1) WS1: where possible, at each date t the individual withdraws 4% of her initial wealth 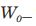with a 2% COLA component adjustment:

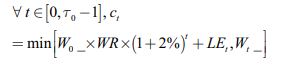
2) WS2: where possible, at each date t she withdraws 4% of her current wealth 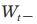minus the cost induced by life events at time t. We fixed a cap such that at time t she cannot withdraw more than 4% of the initial wealth with a 2% COLA component adjustment:

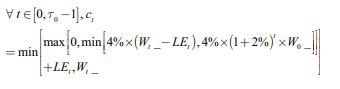
3) WS3: we again consider withdrawal strategy WS1, but add a floor such that, where possible, at time t she cannot withdraw less than 2% of her initial wealth 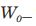with a 2% COLA component adjustment:

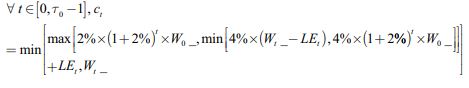
Accounting for life events in WS2 implies that the individual will be ruined before her death in scenarios of the Monte Carlo simulations where the portfolio wealth at time t is such that 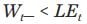(ie, in scenarios where the cost of the life event at time t exceeds the portfolio wealth at time t). WS2 is attractive in so far as, in the absence of life events, it implies a zero probability of the individual outliving their assets, since the amount withdrawn at time t is a percentage of existing wealth. On the other hand, a drawback of this strategy is that it can lead to a high level of uncertainty over withdrawal amounts in dollars over time, depending on the variation of the portfolio wealth. WS3 presents best-ofboth-world characteristics – ie, reasonably low volatility in (real or nominal) withdrawal amounts series over time and a reasonably low probability of the wealth process falling to zero before the individual’s death. The introduction of a floor does not guarantee that the individual (even in the absence of life events) will not outlive her assets, but at least it limits the amplitude of the variations of the withdrawal amounts over time (the presence of the floor allows the individual to benefit from a minimum level of replacement income) and it also decreases the probability of ruin (the presence of the cap prevents individuals from withdrawing excessive amounts at any given points in time).

In addition to these three withdrawal strategies, we also wanted to test two other withdrawal strategies where the percentage of liquid wealth withdrawn at time t depends on the individual’s expected time to live.

Based on Waring and Siegel (2015) and Sun and Webb (2012), we design modular withdrawal strategies where the withdrawal rate at time t is linked to the individual’s remaining time to live. The approach we have adopted is the definition of a glidepath of withdrawal rates as in Sun and Webb (2012), who use tables from the Internal Revenue Service (IRS) that correspond to the inverse of the life expectancy factor. These values – or rather the inverse of these values (see exhibit 2) – can be loosely interpreted as a conservative value for the individual’s time to live.

Exhibit 2 – Glidepath of Withdrawal Rates

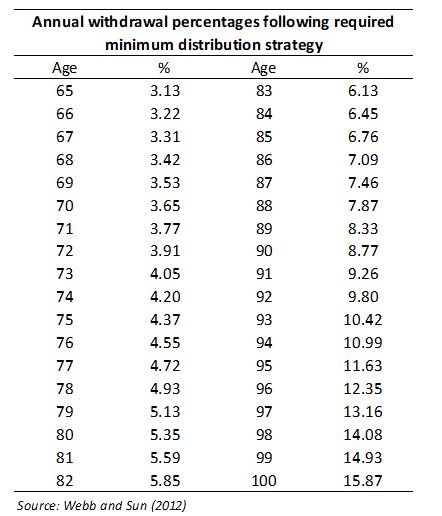
This exhibit reports the withdrawal rates (glidepath) used in Webb and Sun (2012) derived from the IRS tables for required minimum distribution.

The percentages correspond to the inverse of the life expectancy factor in the IRS Uniform Lifetime Table.

It can be loosely interpreted as a conservative value for the individual’s time to live. More details can be found here: https://smartasset.com/retirement/how-to-calculate-rmd

We thus define two additional withdrawal strategies, labelled as WS4 and WS5, where WS4 is defined with a cap and WS5 with a cap and a floor and where for both strategies the amount withdrawn at time t is based on this glidepath. Intuitively, the older the individual is, the less time she can expect to live and the higher the percentage she can withdraw from her account without being ruined. With the notations defined above, the withdrawal amount at time t for WS4 is defined as:

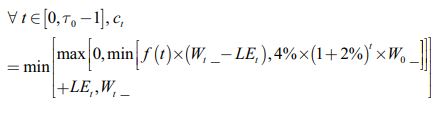
The withdrawal amount for WS5 is: 

Empirical analysis in a balanced fund universe accounting for life events

To compare the different withdrawal strategies, in addition to the welfare function Median (BS) + λVaR5%(ID), which has no intuitive interpretation, we also report key performance and risk indicators:

The additional performance indicator is the Median BPIW (BPIW stands for bequest as percentage of initial wealth), which is the median discounted bequest across all the Monte Carlo scenarios divided by the initial wealth of the individual. This quantity is always positive.

The additional risk indicator, labelled as 5%VaR PLI (PLI stands for percentage of lifetime income), is the fifth percentile across all the Monte Carlo scenarios of the ratio of the discounted realised withdrawals over the discounted target withdrawals. This quantity is always between 0 and 1 and corresponds to the fifth percentile of:

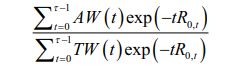
Exhibit 3 shows the median bequest, the fifth percentile of the income deficit, median BPIW and the fifth percentile of the PLI indicators for a universe made up of balanced funds as functions of the weight invested in stocks when considering the five aforementioned withdrawal strategies. Regardless of the equity allocation in the balanced fund, WS2, WS3, WS4 and WS5 display a higher median bequest value than WS1. This result was to be expected since all four strategies systematically involve withdrawal amounts that are lower than or equal to those of the base withdrawal strategy, so it is only logical that they display a higher median bequest compared to withdrawal strategy WS1. More interestingly, when comparing the 5% VaR of the income deficit values of the different strategies, WS3, WS4 and WS5 display better (ie, higher) results than WS2 when the stock weight is higher than or equal to 8%. When we look at the VaR5% PLI chart, we see that (1) WS1 is always the withdrawal strategy with the worst results and (2) WS3 and WS5 are the withdrawal strategies with the best results for a stock weight higher than 15%. Unlike the VaR5% discounted income deficit indicator, which measures in dollars the 5% value-at-risk of the income shortfall, the VaR5% PLI is defined as the fifth percentile value across all scenarios of the ratio between the sum of the individual’s discounted actual withdrawals and the sum of the discounted target withdrawals until death.

Exhibit 3 – Reporting Indicator Charts for the Balanced Fund Universe

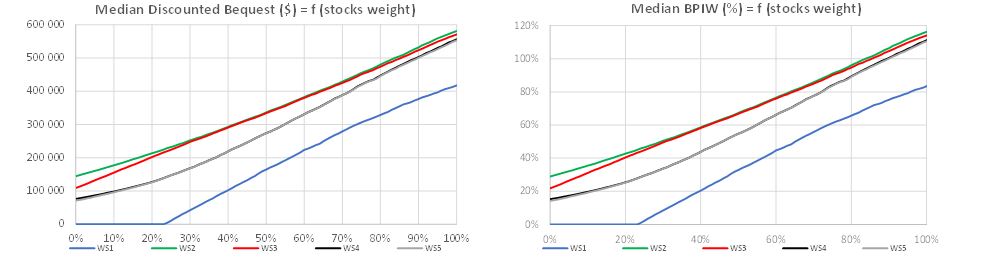
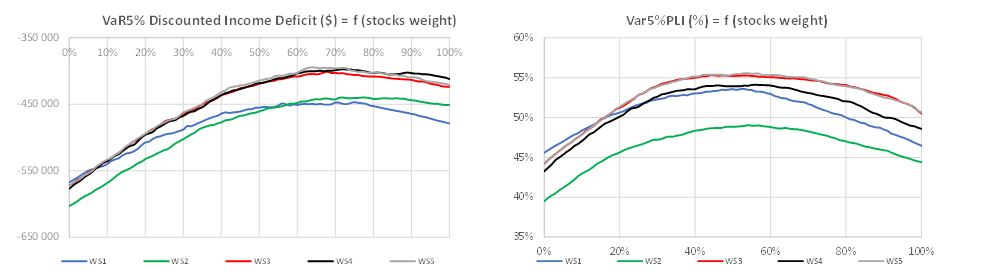
This exhibit reports the charts of the median bequest, median BPIW, VaR5% discounted income deficit and VaR5% PLI indicators f

or a universe made up of balanced funds as functions of the weight invested in stocks with values ranging from 0% to 100%, with a grid step of 1% for the five withdrawal strategies described above. Life events are taken into account.

Exhibit 4 reports the welfare function Median (BS) – λVaR5%(ID) for the five aforementioned withdrawal strategies, for four different values of λ (λ= 1,2,4 and 6) and for a universe made up of balanced funds as functions of the weight invested in stocks. We observe that for all the λ values (except for λ = 6 and a stock weight lower than 8%) and regardless of the stock weight, the welfare function is lower when WS1 is considered. The withdrawal strategy WS3, with both a floor and a cap, appears to be the one that leads to the highest level of investor welfare for most of the possible values of equity allocation in the balanced fund. For a low risk aversion parameter value λ equal to 1, WS3 outperforms WS5 for all stock weights. WS4 and WS5, based on a glidepath that takes into account the individual’s expected time to live, do not lead to better results than WS3. We note that whatever the level of risk aversion, when we set the percentage of equity at a low level, the differences between the welfare function value with the fixed withdrawal strategy and those with the other withdrawal strategies are smaller than when we set the percentage of equity at a high level.

Exhibit 4 – Welfare Function Charts for the Balanced Fund Universe

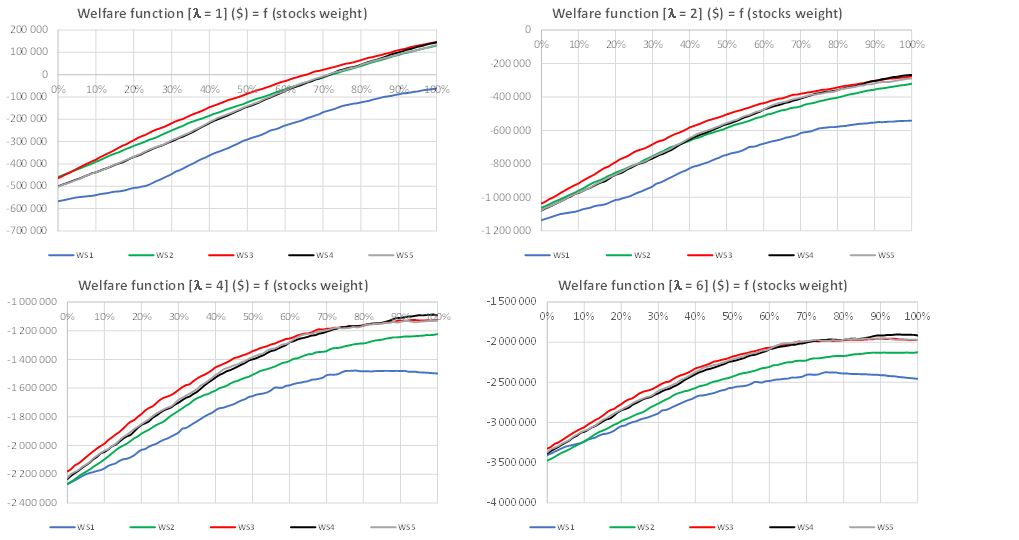
This exhibit reports the charts of the welfare function for four different values of λ ( λ = 1, 2, 4 and 6) for the five withdrawal strategies detailed above

and for a universe made up of balanced funds as functions of the weight invested in stocks with values ranging from 0% to 100%, with a grid step of 1%. Life events are taken into account.

Overall, withdrawing less than the 4% target withdrawal with a 2% COLA indexation in cases where the current wealth is below a certain threshold while (1) guaranteeing a minimum absolute level of withdrawal and (2) imposing a maximum absolute level of withdrawal makes it possible to optimise both performance indicators (ie, median bequest) and risk indicators (5%VaR income deficit), which are the building blocks of the welfare function. 

Conclusion

The first key result from our analysis is that defining the amount withdrawn from the retirement pot at time t as a constant percentage of the liquid wealth at time t (with a cap and possibly a floor) leads to better results compared to a fixed rule in the balanced fund universe for almost every allocation and risk aversion considered. Secondly, it appears that glidepath withdrawal strategies also display better results than the fixed withdrawal strategy with constant (in real terms) withdrawal amounts but are overall outperformed by the flexible withdrawal strategies with a floor. We also found in an analysis not reported here that these results still hold in universes where annuities are available in addition to balanced funds. Overall, we found that state-dependent withdrawal strategies that take into account ‘bad states of the world’ such as poor market performance (low liquid wealth) or high expected time to live display better results than the fixed withdrawal strategy. In practice, additional sources of complexity with joint optimisation of investment and consumption decisions in decumulation are the presence of accounts with multiple tax regimes, other sources of income that have an indirect impact on the tax treatment of the managed wealth, and relocation decisions in retirement that may impact the tax efficiency of investment and withdrawal strategies. We leave these questions for further research. 

The research from which this article was drawn was supported by Bank of America.

Footnotes

[1] These figures are borrowed from the Genworth Cost of Care Survey 2019.

[2] We have chosen to treat lambda risk aversion and equity allocation as two independent degrees of freedom. We acknowledge that we could have refined our analysis by taking into account the fact that a highly risk-averse investor will naturally tend to choose a less aggressive balanced fund than a less risk-averse investor.

References

Bengen, W. P. (1994). Determining Withdrawal Rates Using Historical Data. Journal of Financial Planning 7(4): 171–180.

Maeso, J., L. Martellini, V. Milhau, A. Suri and N. Vrdoljak (2021). A Holistic Goals-Based Investing Framework for Analyzing Efficient Retirement Investment Decisions in the Presence of Long-Term Care Risk. EDHEC-Risk Institute Publication.

Merton, R. (1969). Lifetime Portfolio Selection under Uncertainty: The Continuous-Time Case. Review of Economics and Statistics 51(3): 247–257.

Merton, R. (1971). Optimal Portfolio and Consumption Rules in a Continuous-Time Model. Journal of Economic Theory 3(4): 373–413.

Sun, W., and A. Webb (2012). Can Retirees Base Wealth Withdrawals on the IRS’s Required Minimum Distributions? Center for Retirement Research at Boston College: 12–19.

Suri, A. M., N. Vrdoljak, Y. Liu and R. Zhang (2020). Beyond the 4% Rule-Determining Sustainable Retiree Spending Rates. Merrill Lynch Internal Publication.

Waring, M. B., and L. B. Siegel (2015). The Only Spending Rule Article You Will Ever Need. Financial Analysts Journal 71(1): 91–107.