Maximizing the Benefits of Factor Investing

Industry Analysis

Maximizing the Benefits of Factor Investing

Lionel Martellini
Vincent Milhau

The research from which this article was drawn was produced as part of the Amundi "ETF, Indexing and Smart Beta Investment Strategies" research chair at EDHEC Risk Institute.

• This article provides clarification with respect to the various possible definitions of factors that are relevant in investment practice.
• We develop a framework for allocating to factors in two main contexts, namely allocation decisions at the asset class level, and benchmarking decisions within a given class.
• Several definitions for factors co-exist, which differ through their focus on return versus risk, or on cross-sectional differences between assets versus the time-series properties of assets.
• The various notions of factors are not mutually exclusive and can be combined within a comprehensive framework for factor allocation.
• It is possible to use factor indexes as building blocks and to diversify risk across underlying factors, or to seek to exploit knowledge of economic regimes to design portfolios that react to changes in market conditions.

Factor investing is an investment paradigm under which an investor decides how much to allocate to various factors, as opposed to various securities or asset classes. Its popularity has been growing since the turn of the millennium, especially after the recognition in 2008 that multiple asset classes can experience severe losses at the same time despite their apparent differences. The term “factor,” however, is used with many different meanings depending on the context and the targeted application. The main goal of this article is to provide clarification with respect to the various possible definitions of factors that are relevant in investment practice. This article also develops a framework for allocating to factors in two main contexts, namely allocation decisions at the asset class level, and benchmarking decisions within a given class. For each of these applications, we examine the three most important questions raised by the adoption of a factor investing approach: (i) why think in terms of factors? (ii) what factors should be chosen? and (iii) how do we allocate between them?

Several definitions for factors co-exist, which differ through their focus on return versus risk, or on cross-sectional differences between assets vs. the time-series properties of assets. A distinction can be made between (i) asset pricing factors, (ii) strategies that deliver a positive premium in the long run, (iii) common sources of risk in various assets and (iv) state variables that characterize current business conditions.

Asset pricing theory is concerned with the search of “asset pricing factors,” defined as factors that explain the cross section of expected returns in the following sense: the expected returns of various assets are completely determined by the exposures of these assets to the factors, the exposures being obtained by running a multivariate regression of asset returns on factor values. The premium of a factor measures the incremental reward received in the form of additional expected return by increasing the exposure. According to the theory, it is driven by the covariance between the factor and the “marginal utility of consumption” of the representative agent, which is the gain in utility for a small increase in consumption. A factor is positively rewarded if it tends to be high in “good times,” defined as scenarios in which consumption is high (and consequently marginal utility is low), and low in “bad times,” defined as scenarios in which consumption is low. This is because bearing exposure to this factor tends to generate a high payoff when it is least needed as consumption is already high, and a low payoff when additional money is most valued, meaning that this exposure is unattractive unless it is rewarded by higher return in the long run.

In investment practice, the notion of a factor is more polysemic. A factor can be a profitable strategy that delivers a long-term premium over a benchmark, provided this premium is economically justified as a reward for bearing additional risk, like in asset pricing theory, or as the result of biases in investors’ behavior that cannot be completely eliminated due to the existence of limits to arbitrage. This definition applies well to the passive equity strategies that select stocks based on some observable characteristic: low size, high value, high momentum, low volatility, high profitability and low investment are sources of long-term returns documented by extensive academic research and backed by sound economic rationale. Capturing these premia at reasonable cost is the goal of “equity factor indexes” offered by equity index providers. In non-equity classes, research is more recent, so our understanding of risk premia is comparatively more limited. Value, momentum and carry are three effects that have been reported for bonds and commodity and currency futures, but the list is likely still incomplete, and further research is needed to study the existence and the persistence of rewarded factors, in particular in fixed income securities, which is a major asset class for institutional investors.

Another notion of a factor is that of the risk factor, and it refers to common sources of risk that affect various securities or asset classes. Volatilities and correlations are then mainly explained by the exposures to these factors, and common exposures can result in joint losses in severe bear markets, such as in 2008. Several macroeconomic variables such as output, growth and inflation can play this role, but in order to maximize the explanatory power, risk factors are often taken to be implicit — that is, they are extracted from asset returns by statistical analysis. In the Barra equity model, implicit factors are intended to represent the common sources of risk that affect assets with similar microeconomic characteristics. Specific statistical procedures can also be used to obtain factors with a zero correlation, a property that facilitates the decomposition of the risk of a portfolio. These procedures are named principal component analysis and minimum linear torsion (see Carli, Deguest and Martellini (2014) for a review, and the example of implementation below).

Finally, a third possible definition for a factor in practice is as a state variable that contributes to explaining time variation in the risk premia, volatilities and correlations of assets. This definition takes a time-series perspective, unlike the previous ones, which aim to explain cross-sectional properties. The risk and return characteristics of assets can be compared across regimes defined in terms of macroeconomic variables that have an impact on discount rates or expected future cash flows. It is also standard practice to take state variables as the dividend yield as a predictor of stock returns, or use the forward-spot spread to predict bond returns.

It should be noted that financial theory establishes connections between the three practical categories of factors and the notion of the pricing factor: the risk-based explanation for the profitability of passive strategies is that they are exposed to rewarded pricing factors, the Arbitrage Pricing Theory of Ross shows that common risk factors can be pricing factors, and the Intertemporal Capital Asset Pricing Model of Merton implies that state variables that predict changes in investment opportunities are pricing factors

At the asset class level, risk factors allow the diversification of a portfolio to be assessed in a more meaningful way than dollar weights, and they are involved in the construction of liability-hedging portfolios by factor matching techniques. Conditioning factors are useful to design performance-seeking portfolios that react to market conditions.

Modern portfolio theory gives a clear definition of what a “well-diversified” portfolio should be: it should have the highest Sharpe ratio, equal to the reward, measured as expected excess return over the risk-free rate, per unit of risk, measured as volatility. But this prescription is hard to implement in practice, due to the strong uncertainty over expected return estimates, which research has shown to have a dramatic impact on performance. To alleviate the concern over parameter uncertainty, one may decide to go back to conventional wisdom and diversify by “spreading eggs across baskets,” which hopefully leads to more efficient collection of risk premia across assets. A standard interpretation of this principle is to weight constituents equally, but it opens the door to portfolios with concentrated risk: the risk of a 50%-50% stock-bond portfolio is mostly explained by stocks. Factor contributions are easiest to calculate when the factors are uncorrelated from each other because there are then no cross-correlation terms to divide between factors. As introduced earlier, uncorrelated risk factors that completely explain uncertainty in a given universe can be obtained by (at least) two statistical procedures, namely principal component analysis (PCA) and minimum linear torsion (MLT). The latter method was introduced more recently, and it aims to address some of the shortcomings of PCA by minimizing the distortion of factors with respect to the original assets: this property facilitates the economic interpretation of factors and enhances robustness across samples.

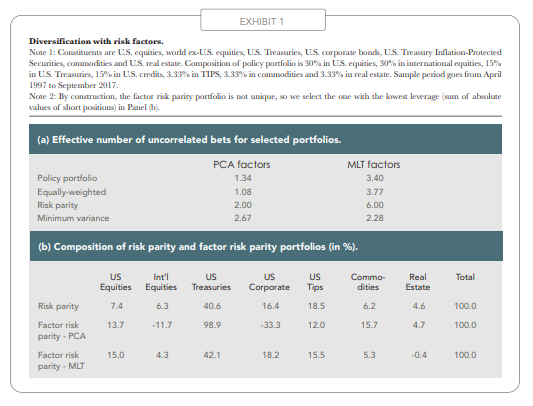
Exhibit 1 shows an example of the ENUB calculation in a seven-asset class universe mixing equities, bonds, commodities and real estate. The four benchmark portfolios have ENUBs much lower than the theoretical maximum of seven, which means that their risk is concentrated in a few risk factors, except for the risk parity allocation when MLT factors are employed; indeed, each MLT factor is close to an asset, so the risk parity portfolio should not be exceedingly far from a factor risk parity portfolio. Nevertheless, the true factor risk parity portfolio for MLT factors has a different composition than the risk parity one. With PCA factors, it is virtually impossible to achieve factor risk parity with a long-only allocation, since the first factor will inevitably dominate the others, so sizeable short positions must be taken. This example illustrates the fact that MLT factors are computationally easier to handle.

Risk factors are also naturally involved in a different context, where the objective is not to efficiently diversify across assets, but to replicate a benchmark as closely as possible, like in asset-liability management, where a good liability-hedging portfolio (LHP) is needed. Through the discounting mechanism of future cash flows, interest rate risk is a major source of risk, and often the dominant one, in liabilities, so aligning the interest rate exposures of assets and liabilities is the first step toward the construction of a LHP. The difficulty here is that exposures are not linear, so linear approximations are needed. The first-order approximation leads to duration matching, which is effective at immunizing the funding ratio against small changes in the yield curve, but in order to hedge against the effects of larger changes, finer approximation is required, involving a matching of convexities in addition to duration alignment.

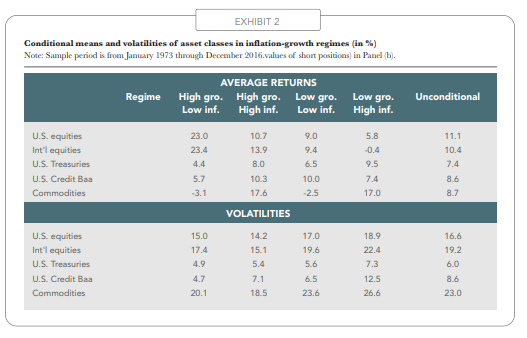
Beyond risk factors, state variables characterizing timevarying investment opportunities may prove useful in asset allocation, in order to construct a performance-seeking portfolio (PSP) that adapts to market conditions. A simple way to define regimes is to look at inflation and growth in gross domestic product and to make a distinction between four regimes, depending on whether inflation and growth are below or above their mean values. The results in Exhibit 2 show that equities do best when inflation is modest and growth is dynamic, while the low growth and high inflation regime is the least favorable to them, both in terms of performance and volatility. Commodities perform better in the high inflation than in the low inflation periods, and Treasuries deliver their best performance in the low growth and high inflation regime, thereby confirming their role of a “safe haven.” These results suggest that regimes of growth and inflation can be used to adapt the relative weighting of asset classes as a function of market conditions.

By equating the contributions of assets to risk, the risk parity approach to allocation is a big step toward addressing this issue, but it still misses the fact that constituents are exposed to common sources of risk. To assess the level of diversification of a portfolio in terms of risk factors, we propose to calculate the effective number of uncorrelated bets (ENUB), a quantitative measure of the deconcentration of factor contributions to portfolio volatility that is minimal when risk is concentrated in a single factor, and maximal when all factors contribute equally to risk. The latter condition defines a factor risk parity portfolio.

Within an asset class, theory makes a case for factor investing by showing that the maximum Sharpe ratio (MSR) portfolio of individual securities coincides with the MSR portfolio of pricing factors, no matter how large the original universe is. Empirically, equity factor indexes representing the six well-documented factors (size, value, momentum, volatility, profitability and investment) dominate the standard capweighted index in terms of risk-adjusted return, especially if they are “smart weighted.” Further improvement over the risk-return characteristics of individual factors is achieved by building multi-factor portfolios.

Going back to the theoretical definition of a well-diversified portfolio as the maximum Sharpe ratio (MSR) portfolio, a theoretical result that we prove in this paper is that the MSR portfolio of any set of assets coincides with the MSR portfolio of factors, provided the latter are pricing factors in the sense of asset pricing theory. This result holds regardless of the number of assets, so it represents a substantial reduction in dimensionality if there are many of them, as is generally the case in benchmarking. It also provides the optimal form of the “two-step process,” in which an allocation exercise to multiple securities is divided into two steps, namely the grouping of securities in benchmarks, and then an allocation to the benchmarks.

This theoretical result cannot be directly applied in practice to calculate the MSR portfolio because a complete set of pricing factors is not known, but the idea of dimension reduction can be exploited with other types of factors, namely risk factors. Indeed, under a factor model, each return can be decomposed into a systematic part that is a sum of factor exposures, plus an idiosyncratic term, and provided idiosyncratic returns are uncorrelated across assets, the number of independent parameters to estimate in the covariance matrix is much smaller than if no factor structure is postulated. Considering, for instance, a universe of N = 500 stocks, it is shown in the paper that the number of covariances is 125,250 without a factor model, 3,521 with six factors and 2,006 with three of them. In other words, the use of risk factors alleviates the curse of dimensionality for the estimation of the covariance matrix. This idea is implemented in BARRA models, as explained in the Barra Risk Model Handbook.

Though a comprehensive set of pricing factors has not been uncovered to date, it is well known from a large body of empirical research that at least in the equity class, factors understood as profitable strategies provide a substantial improvement over the standard cap-weighted index in terms of risk-return characteristics. Exhibit 3 summarizes this evidence by assuming factors to be a set of long-only factor indexes made of stocks with a given characteristic: mid-market capitalization, high book-to-market, high past one-year return, low volatility, high gross profit-to-asset ratio or low total asset growth. The base case version of these indexes is capweighted, but “smart factor indexes” deviate from this weighting scheme in order to better diversify away unrewarded risk. Among the many possible schemes, the table considers equal weighting and inverse volatility weighting. Over the long period considered, all factor indexes outperform the broad cap-weighted index and display a higher Sharpe ratio, and the smart versions bring further improvement on these figures.

The equivalence result between the MSR portfolio of securities and the MSR portfolio of pricing factors suggests that it is interesting to combine factors. Thus, the next exercise that we conduct consists of the construction of multi-factor equity portfolios. Exhibit 4 shows statistics for selected allocations. Given that the six factors are long only, they are all exposed to the market equity factor and they have high correlations, greater than 90%, so one may wonder what benefits can be expected from mixing such highly correlated constituents. It turns out that the annualized long-term return and the Sharpe ratio are only marginally improved with respect to the average properties of the constituents, but the relative analytics, which measure risk and return with respect to the broad cap-weighted index, are much more favorably impacted. This can be attributed to the fact that the relative correlations — that is, the correlations between excess returns — are much lower than the absolute correlations and are often negative, so diversification can be expected to be more effective from a relative perspective. In particular, the equally-weighted portfolio has much lower tracking error and a maximum relative drawdown, as well as a much higher information ratio than the average of the constituents.

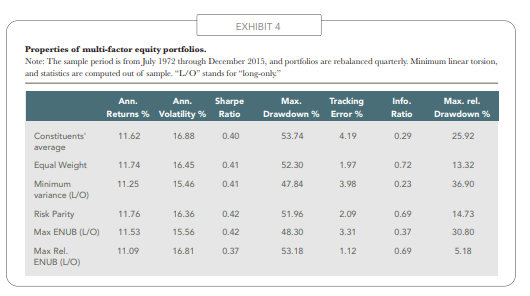
The choice of the allocation method has important effects on the properties of the multi-factor portfolios.

The global minimum variance portfolio achieves its objective even on an out-of-sample basis, but does so at the cost of sizeable relative risk, while the equally-weighted portfolio displays a higher volatility, but better relative analytics. We also calculate two portfolios that maximize diversification in terms of risk factors (subject to a long-only constraint). At this stage, two notions of factors are involved — on the one hand, constituents are profitable passive equity strategies, and on the other, the weighting scheme seeks to maximize diversification in terms of underlying risk factors. The latter factors are extracted successively from the covariance matrix of the constituents and from their relative covariance matrix, which collects the covariances of excess returns. Each system of factors gives rise to its own value for the ENUB, and the two ENUBs respectively measure the deconcentration of the volatility and the tracking error. The maximum relative ENUB portfolio has lower relative risk, measured either through the tracking error or the relative drawdown, than its absolute counterpart. Additional backtests — the results of which are not reported here but can be found in the complete version of this article — show that this finding is robust to the choice of the sample period.

As a conclusion, the various notions of factors are not mutually exclusive and can be combined within a comprehensive framework for factor allocation. Further research is needed to improve our understanding of their interactions, especially in the fixed-income class.

As we argue in the previous empirical illustration, a factor allocation exercise can involve more than one notion of factors. It is possible to use factor indexes as building blocks and to diversify risk across underlying factors, or to seek to exploit knowledge of economic regimes to design portfolios that react to changes in market conditions. After five decades of research on equities, robust sources of profitability are now well identified in this class, but not as well in other classes, especially in fixedincome. Moreover, while past research has mostly focused on finding predictors for the equity market or the bond market as a whole, and while it is recognized that factor indexes have cyclical behavior, further investigation is needed to quantify the degree of predictability in these factors and to identify relevant predictors.

References

• Carli, T., Deguest, R. and Martellini, L. 2014. Improved Risk Reporting with Factor-Based Diversification Measures. EDHEC-Risk Institute Publication.
• Merton, R. 1973. An Intertemporal Capital Asset Pricing Model. Econometrica 41(5): 867–887.
• Martellini, L. and Milhau. V. 2018.Smart Beta and Beyond. Maximising the Benefits of Factor Investing. EDHEC-Risk Institute Publication.
• Ross, S. 1976. The Arbitrage Theory of Capital Asset Pricing. Journal of Economic Theory 13(3): 341–360.