Why Alternative Indices

Toward a new paradigm for alternative investment

From an absolute performance logic….

Wanting to use hedge funds as a risk diversification tool presupposes that we have mastery over the issues at stake in the control of hedge fund risks. Even though recent research has given us a better understanding of the subject, it is certainly the area in which the most progress remains to be made. As stressed by, for example, Lo (2001) , Amenc, Martellini, Vaissié (2003) and Fung and Hsieh (2001) , there are at least three reasons for alternative funds posing specific problems for measuring and controlling risks:

 difficulties in taking the credit and liquidity risk dimensions into account  difficulty in developing relevant benchmarks  difficulties in accounting for the dynamic and non-linear aspects of alternative risk.

While nearly all hedge funds highlight a so-called “absolute return” policy, the risk-free rate is only a good benchmark if the following two conditions are respected:

 assumption 1: the fund has a market beta equal to zero  assumption 2: the CAPM (an equilibrium model proposed by Sharpe in 1964) is an appropriate model for the alternative universe.

While the first assumption is respected for certain types of alternative funds, such as equity market neutral or fixed-income arbitrage (i.e. Relative Value strategies in general), it is certainly not valid for the other categories (Long/Short, Short Selling, Funds of Funds).

The second assumption is even more debatable. In order to have a better comprehension of the issues at stake in the performance of alternative funds, it is important to understand first of all that the excess return of a risky portfolio compared to the risk-free rate, as it is measured for a given sample, can, in general, come from three distinct sources, as described in the following equation:

Excess return of the portfolio = normal return + abnormal return + statistical noise

The first term, the “normal” return, corresponds to the market’s fair reward for the risks to which the portfolio is exposed. It is therefore a premium (or premiums) for the risk(s), which can be evaluated with the help of a single factor model like the CAPM or with the help of a more general, multifactor model, justified on the theoretical side through equilibrium (Merton, 1973) or arbitrage (Ross, 1976) reasoning, and implemented in the business world by a certain number of firms such as, for example, BIRR, Quantal, Aptimum and BARRA

In the alternative universe, as we mentioned earlier, recent research has highlighted the inadequacy of the CAPM and underlined the exposure of alternative returns to factors such as volatility risk, default risk and liquidity risk.

It is therefore wrong to state that a non-directional alternative strategy, i.e. a strategy that is not exposed to market risk (for example, fixed-income arbitrage, convertible arbitrage or zero-beta strategies), should be rewarded at the risk-free rate. That is an overly restrictive application of a single factor model (the CAPM) which does not allow for a good description of the behaviour of alternative funds. Since hedge funds, as a general rule, have a low level of correlation with the market, using the CAPM is effectively much the same as comparing their performance to the risk-free rate. However financial risks, particularly in the alternative world, are generally multiform, and, consequently, there must be multiple risk premiums. For example, a mean return of 10% for a non-directional fund like LTCM, when that of the risk-free rate is 4%, does not necessarily reflect an abnormal return of 6%. Within the 6%, there could be volatility, liquidity or default risk premiums (or any other risk factor, the existence of which may have escaped the wisdom of the modellers, that is rewarded by the market at equilibrium). In total, the abnormal return, the fund’s alpha, could very well be positive, negative or nil!

Moreover, the dynamic character of alternative strategies also leads to an evolution in the exposures to the multiple risk factors. This evolution will vary in importance depending on the strategy studied. A static (i.e. single period) model like the CAPM does not allow us to account for that. In fact, it can only reveal the average exposure, recorded over the observation period, of hedge fund performances to the market risk. For example, if the performances of a strategy have a sensitivity (i.e. a beta) of 0.40 to the market risk when the market risk rises, and 1.00 when it falls, the regression coefficient will be 0.70 (if we consider that there have been as many rising periods as falling periods over the observation period). However, a beta of 0.70 in no way reflects the true exposure of the strategy in question to the market risk.

As a consequence of the exposure of hedge funds to multiple risk sources and the dynamic character of the management of hedge funds, absolute performance measurement instruments, such as the Sharpe ratio, are equally inappropriate for evaluating the performance of alternative funds. Although the ratio has the advantage of being simple, robust, and above all, not depending on any reference index, it does not allow the risk of alternative strategies to be captured satisfactorily. The Sharpe ratio, for example, completely hides the existence of third and fourth order moments (i.e. skewness and kurtosis), which are nonetheless frequently unfavorable to the investor in the alternative world. By only considering the first and second order moments of the distribution function of hedge fund performances a large part of the risk being run is ignored. In this area, certain authors have shown that the low level of volatility of numerous alternative strategies is only obtained in exchange for fatter distribution tails. The price to be paid for risk-adjusted performances that seem to be significantly better than those of traditional assets is therefore an increased probability of having to put up with extreme losses (notably due to liquidity and credit risk). To this is added the ease with which it is possible to manipulate the Sharpe ratio by transferring part of the risk from the first and second order moments to the third and fourth order moments (cf. “short volatility strategies” or “truncated return strategies”).

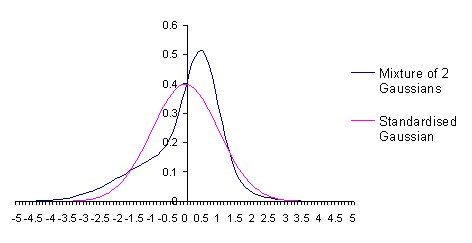
For example (cf. Amenc, Martellini, Vaissié (2003)), an equally weighted mixture of a Gaussian with a mean of 0.5 and a standard deviation of 0.5 and a Gaussian with a mean of –0.5 and a standard deviation 1.32 exhibits the same mean and variance as a standardised Gaussian (0 and 1, respectively), but a skewness of –0.75 and a kurtosis of 6.06, compared to 0 and 3, respectively, for the standardised Gaussian (see graph below). Only by taking into account the third and fourth order moments can we truly distinguish the funds with returns that follow those probability distributions.

…. towards a relative performance logic

The non-linear exposure of hedge funds to multiple risk factors poses numerous problems for evaluating their performance with linear models such as the CAPM. Constructing replication portfolios made up of stocks, bonds and especially derivative instruments is one of the ways explored by researchers. It has been shown by authors such as Naik and Agarwal, Mitchell and Pulvino and Fung and Hsieh that introducing non-linear risk factors (i.e. derivatives) allows part of the non-linearity of hedge fund performances to be captured. Using that observation as a starting point, numerous studies have been carried out in order to establish reliable methods for replicating the different hedge fund strategies (cf. Gatev, Goetzmann and Rouwenhorst (1999), Mitchell and Pulvino (2001) or Agarwal and Naik (2001)). The indexes constructed by T. Schneeweis and H. Kazemi at the CISDM (Center for International Securities and Derivatives Markets) illustrate this concept of passive indexes perfectly (strategies concerned: Convertible Arbitrage, Distressed Securities, Equity Hedge, Market Neutral, Fixed Income, Macro and Relative Value). These indexes, constructed from liquid securities (stocks, bonds, index or equity derivatives, etc.), do not contain hedge funds. They are consequently used more as replication portfolios intended for investing, or benchmarks for evaluating the performance of individual managers, than hedge fund indexes in the true sense. Passive replication seems to offer promising results, but remains today in the domain of academic research.

A pragmatic alternative to developing factor models involves comparing the return of a given fund to that of a portfolio of funds following the same strategy (peer benchmarking), or to that of a representative index (index benchmarking). It seems therefore that the alternative investment industry is in the process of switching from an “absolute return” logic (where the benchmark is the risk-free rate) to a “relative return” logic (where the benchmark is a portfolio of funds following a comparable strategy).

What remains to be determined is which index to use. The difficulties related to the development of quality indexes, which are already evident in the traditional universe, are exacerbated in the alternative investment world, in the areas of both representativeness and purity.